How fast is bitcoin’s price going to increase in the long-term? A popular model called the stock-to-flow model forecasts non-diminishing returns: According to this model, bitcoin’s price is expected to increase approximately ten-fold every four years.
The authors of this article have each proposed a competing model based on time as an input variable (here and here) that forecasts diminishing returns in the long term. Our models forecast continuing price growth for bitcoin, but at a slower and slower rate. One of us has noted that independently of the model used, diminishing returns have so far been observed in all of bitcoin’s history.
The difference between the two classes of models leads to wildly different forecasts for the long-term.
In this article, we examine where the difference in long-term forecasts between the time and the stock-to-flow models come from. We will decompose the input variable of the stock-to-flow model into parts and see that one of these components leads to the price growth to be non-diminishing. We will also see that if this component is allowed to be weighted separately in order to best fit bitcoin’s realized price history, we obtain a model with diminishing returns.
The new price models examined in this article should not be interpreted as accurate forecasts of future bitcoin prices, but they to allow us to better understand bitcoin’s price evolution. We find indications that the time-based models are somewhat too bullish, and the stock-to-flow model even more so.
The authors of this article have each proposed a bitcoin price model that uses time as an input variable. The motivation of these models is that the price appears very linear in a log-log plot. The price is modeled as
![]() ,
,
where time refers to the time passed since a given event in time such as the genesis block. The variables a and b are found via regression in such a way as to best fit bitcoin’s realized price data.
A different price model known as the stock-to-flow model has been described in Modeling Bitcoin’s Value with Scarcity, in which the price of bitcoin is determined by the stock-to-flow value of bitcoin, which is a measure of scarcity and programmatically pre-determined. There price is here modeled with a very similar equation, but uses a different input variable. The model equation is:
![]() ,
,
where S2F refers to the stock-to-flow value, and c and d are found via regression.
The two models look superficially very similar: both predict the price of bitcoin based on the logarithm of its underlying variable. The difference in the models comes solely from the use of a different input variable. The choice of the input variable leads to wildly different price forecasts, with the stock-to-flow model producing much more bullish forecasts than the time-based model.
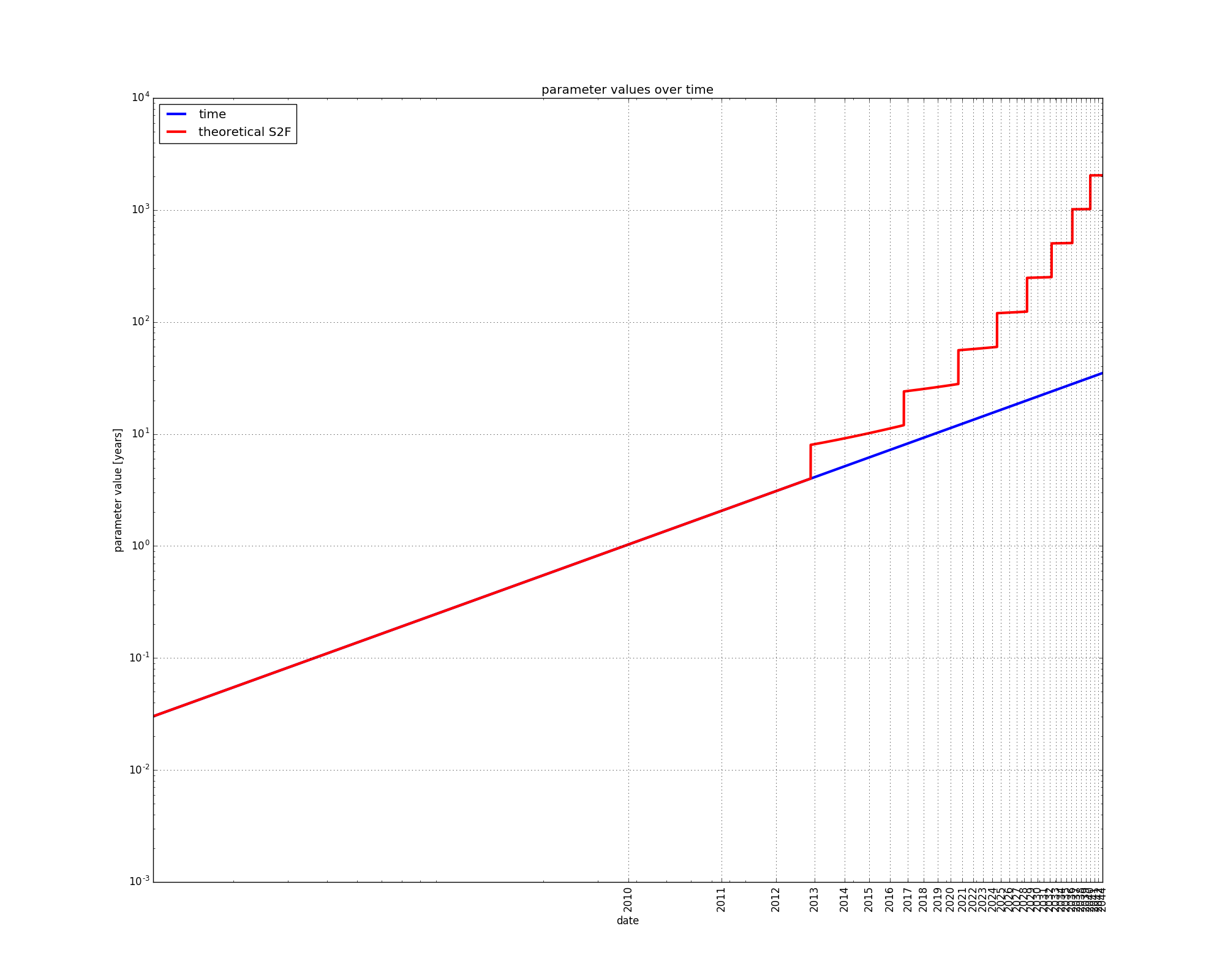
Every ten minutes on average, a bitcoin block is mined, and a number of new bitcoins are put into circulation. The emission schedule has been defined ahead of time. The number of newly created bitcoins in each new block is cut in half every four years. The number of already existing coins are sometimes referred to “stock”, whereas the flow of newly created coins can be referred to simply as “flow”. The ratio of newly created coins over the total stock of existing coins is referred to as the “stock-to-flow” measure, or S2F for short.
![]()
since the stock of existing coins keeps increasing, and the number of newly mined coins is divided in half every four years, the S2F measure increases, and has steep steps every four years:
Michael P. Frank proposed to model the S2F measure using an analytical formula which disregards the step shape, but otherwise approximates the S2F measure. He then decomposes this analytic S2F representation using a Taylor series expansion, the first component of which is time itself. We borrow his approach in this article. 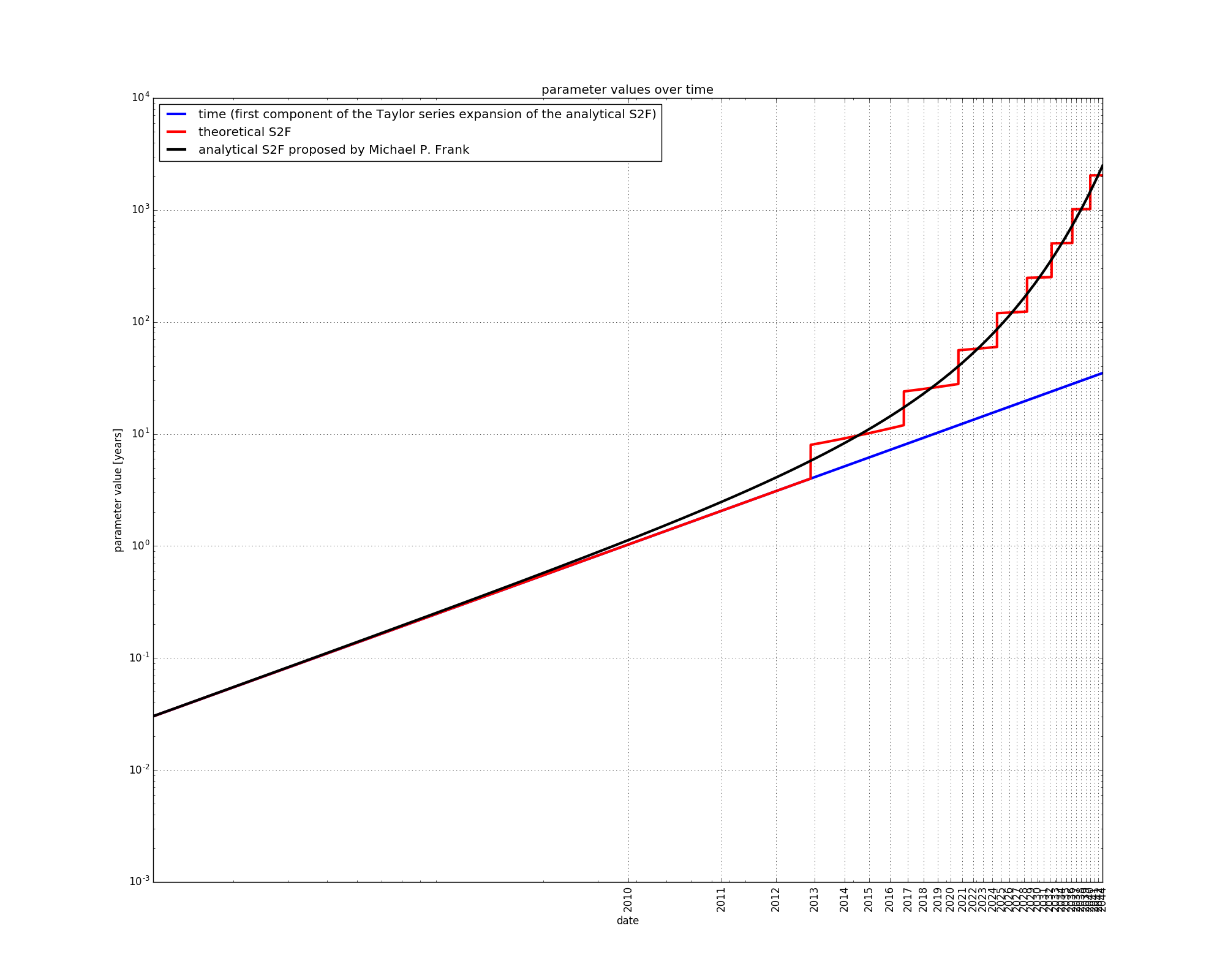
The analytical S2F approximates the S2F measure quite well. The part of the S2F which is not explained by the analytical S2F is a residual which we will call “steps”:
![]()
The S2F measure is then exactly given by:
![]()
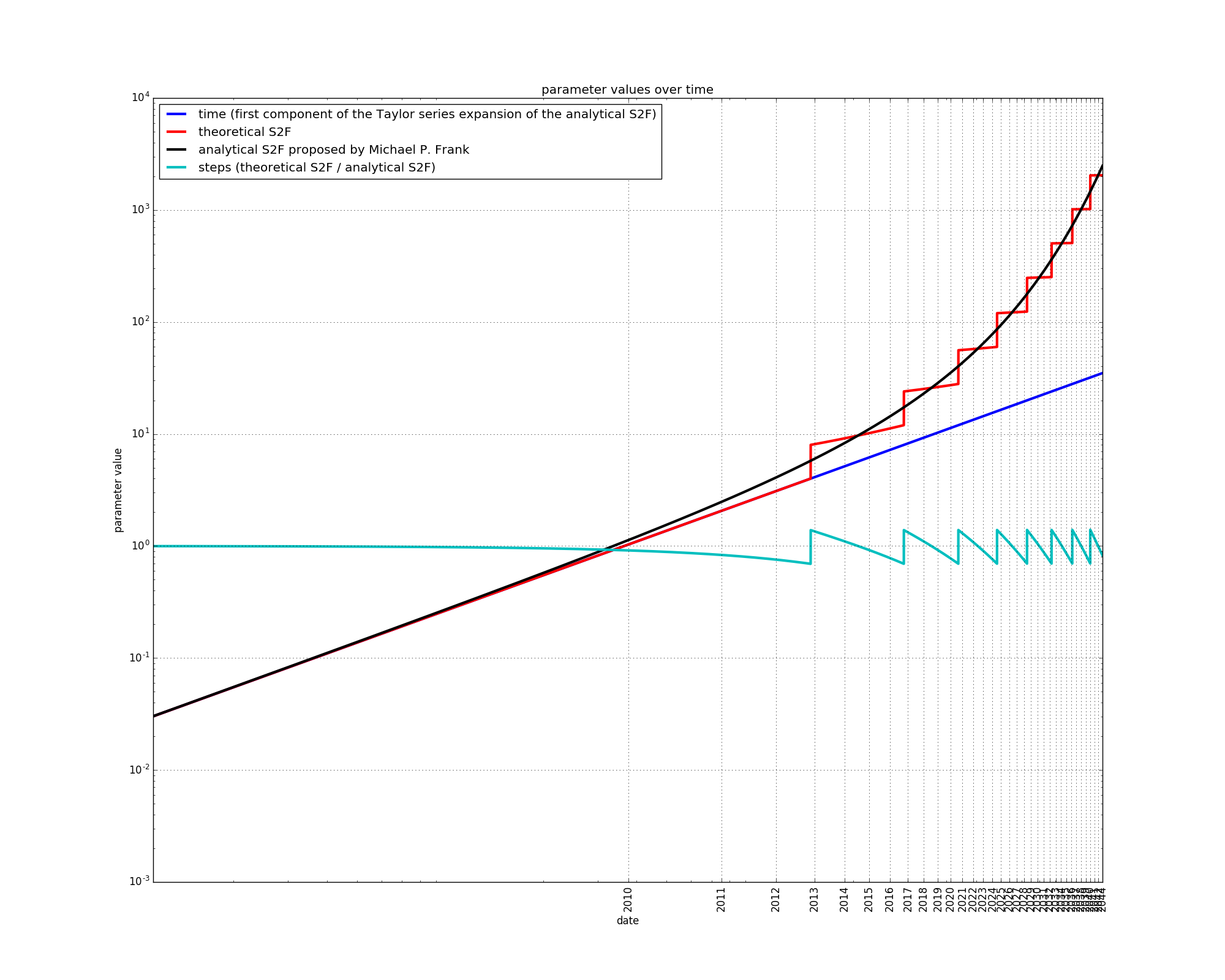
Let’s take a closer look at Michael P. Frank ’s analytical S2F.
The daily flow of new coins can be approximated by:
![]() ,
,
where ![]() , and
, and ![]() . The constant
. The constant ![]() comes from the fact that bitcoin halvings occur every approximately four years, whereas the constant
comes from the fact that bitcoin halvings occur every approximately four years, whereas the constant ![]() comes from the fact that the original block reward was 50 new bitcoin per block (every ten minutes).
comes from the fact that the original block reward was 50 new bitcoin per block (every ten minutes).
The analytical daily flow of new coins at day ![]() is:
is:
![]() ,
,
new bitcoins per day, which corresponds to 50 bitcoins mined every ten minutes, as expected. The daily flow then decreases, e.g. after four years:
![]() ,
,
the flow is exactly halved, also as expected. The analytical flow is a smooth approximation of the theoretical flow, which behaves in a step-wise fashion.
The stock, or total supply of coins on a given day ![]() after the genesis block can be found by integrating the daily flow over days:
after the genesis block can be found by integrating the daily flow over days:
![]()
The analytical S2F is equal to the analytical stock divided by the analytical flow:
![]() .
.
Simplifying:
![]() .
.
We now have a smooth approximation of the S2F values, as already proposed by Michael P. Frank.
The analytical S2F can be decomposed using a Taylor series expansion:
![]() .
.
It is interesting that the first component of the Taylor series expansion is proportional to d (time in days), whereas the subsequent terms are proportional to higher powers of d. We will express the sum of the Taylor series components that have a higher power of d using a single variable, the “higher powers” variable:
![]() .
.
The analytical S2F can therefore be expressed as the sum of time in years plus a “higher powers” variable that is proportional to higher powers of d.
The fact that time is the first component of the Taylor-series expansion of S2F means that time is a good initial approximation of S2F. This time-based and S2F-based price models are therefore inherently linked.
Alternatively, the analyltical S2F can be expressed as the product of two terms: time, and a second variable which we will call “aggressive”.
![]() ,
,
where the aggressive variable is given by:
![]()
At first, the analytical S2F is adequately approximated by the time variable, but the two variables diverge later on. This is expected since time is the first component of the Taylor series expansion of the analytical S2F. The divergence between time and the analytical S2F is due to the “aggressive” variable.
![]() .
.
Plugging the “aggressive” variable into the previous expression for S2F gives us:
![]()
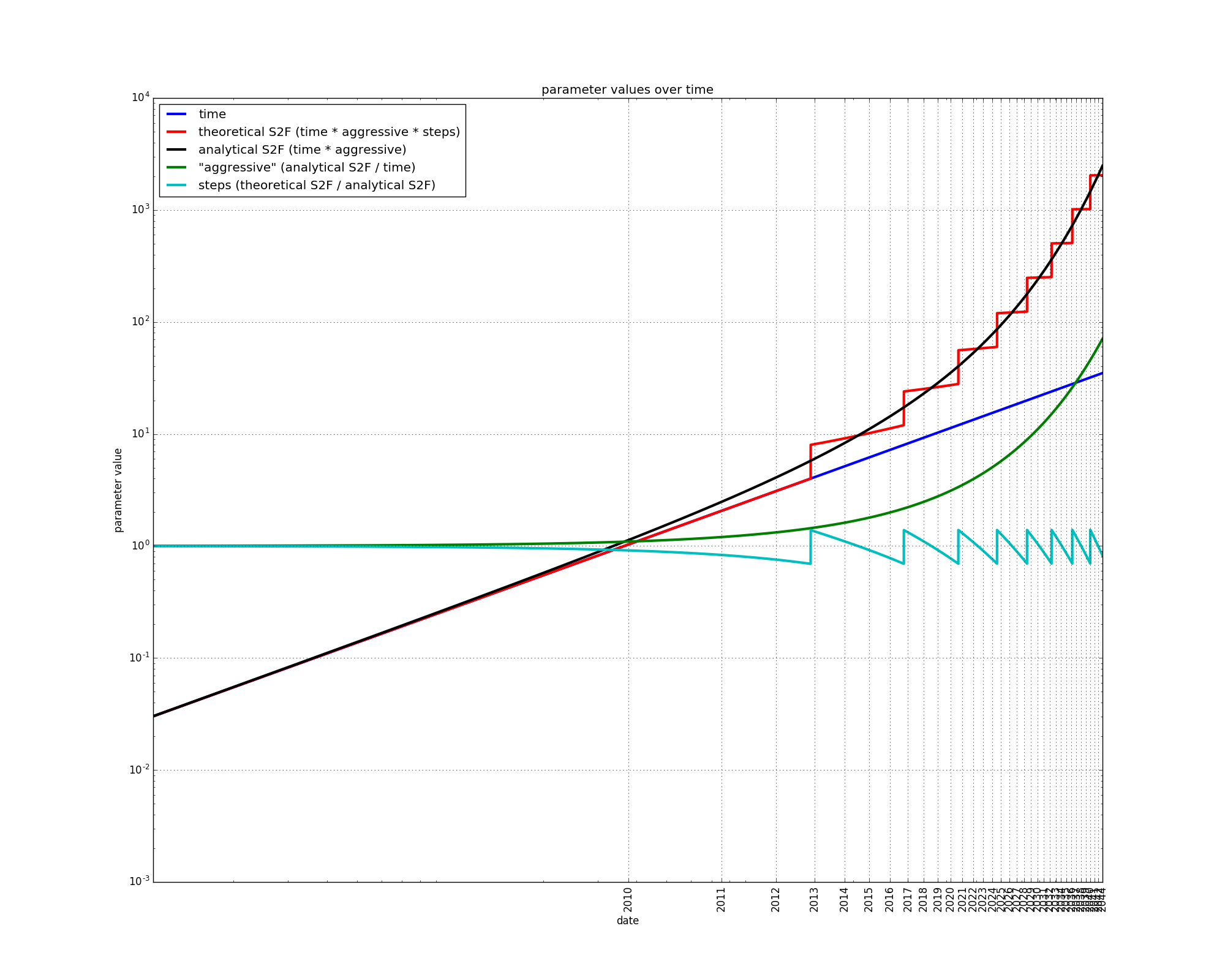
In a log-log plot, the aggressive variable has an “upward” curvature. It grows slowly at first, and then faster and faster: it ramps up.
Using the above, the stock-to-flow price model
![]()
can be exactly rewritten as
![]() ,
,
which in turn is exactly equivalent to:
![]() ,
,
or:
![]() .
.
Reformulating the S2F model in this way is interesting because it makes the link between the S2F-based and time-based model (which is inherent due to the Taylor-series approximation) more visible. The two remaining components are:
As an experiment, we will allow each component of the S2F model to receive a different weight, so that the original S2F price model
![]()
becomes:
![]() ,
,
where ![]() ,
, ![]() , and
, and ![]() are all found via regression and need not necessarily be equal to each other. Let’s call this model the “decomposed S2F model”.
are all found via regression and need not necessarily be equal to each other. Let’s call this model the “decomposed S2F model”.
We will also consider a “decomposed S2F model without steps”:
![]() ,
,
which does not take into account the “step” signal.
We now have five models to compare:
For each of these models, the parameters are found via ordinary least squares (OLS), using bitcoin’s price history since prices have been publicly listed by exchanges (17th of July 2010). Some prices can be found for the year 2009, but these datapoints will not be used in our regression. We obtain the following results:
![]()
![]()
![]()
![]()
![]()
Two things should be noted immediately:
In the two decomposed S2F models, each component receives a different weight. This means that it is possible to obtain a better fit to the data by allowing each component of the S2F variable to be weighted differently.
The “aggressive” variable is negatively weighted in both decomposed S2F models. This is different from the S2F model, in which the aggressive variable component receives a positive weight (the same weight as for the other two S2F components).
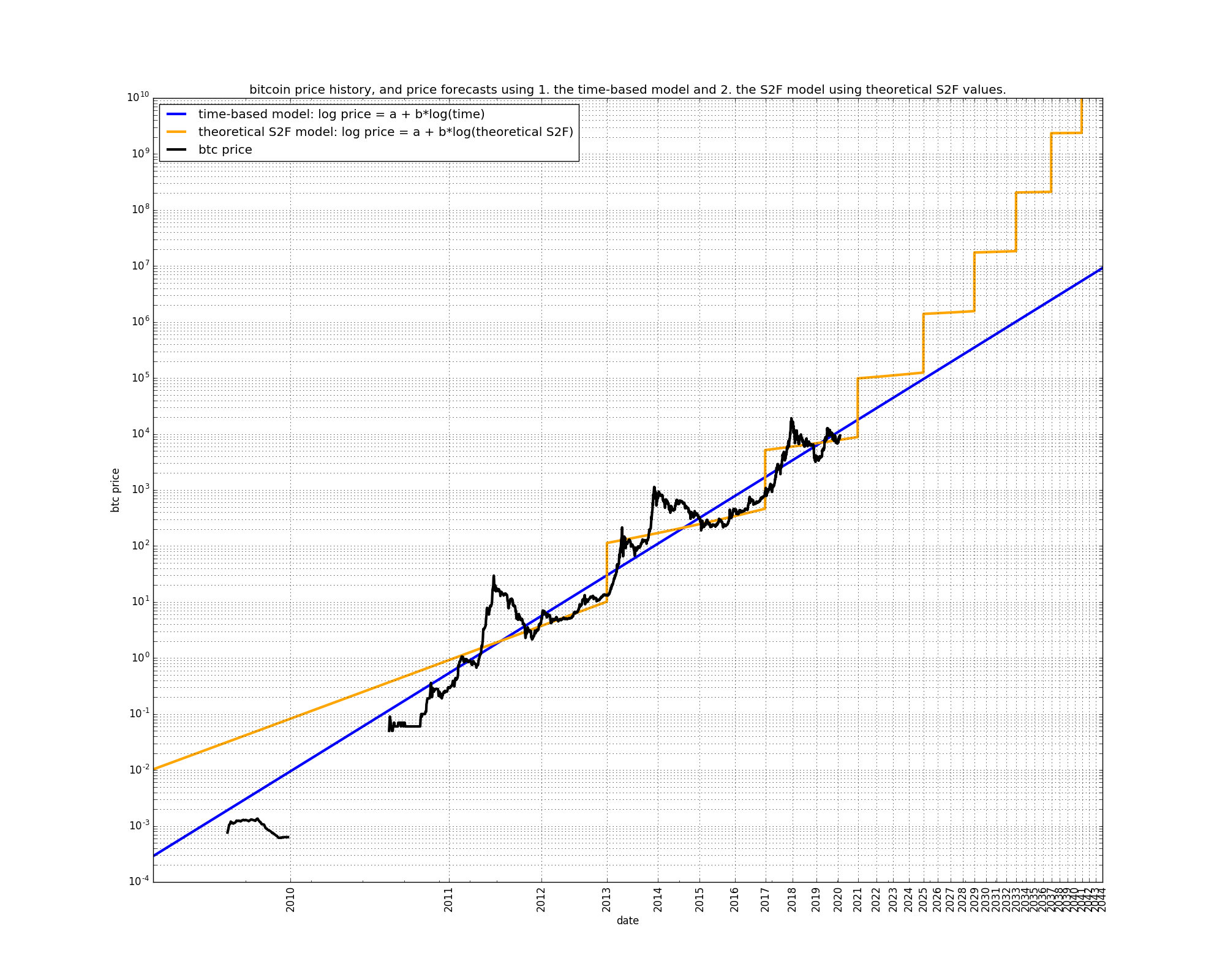
Let’s plot the five price models along the realized price data on the same graph in log-log scale:
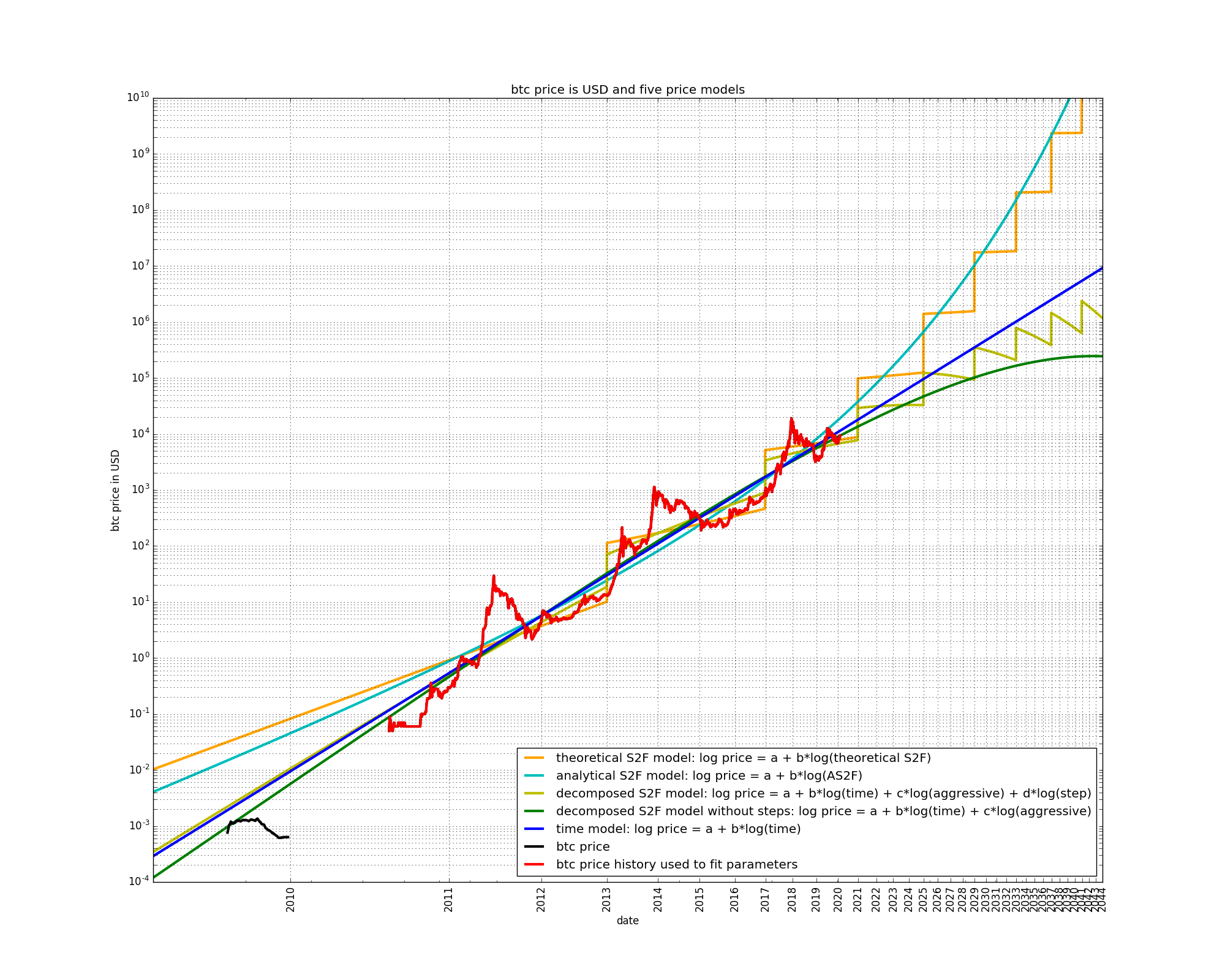
The time-based model is a straight line in a log-log plot, as explained in previous articles.
The S2F model at first grows slower than the time-based model, but then increases its growth rate, and then grows faster than the time-based model. Starting at the next (third) halving, the growth rate stays approximately constant at roughly ten-fold returns every four years. The precise numbers for the S2F model are somewhat different here to those listed elsewhere because we have used theoretical S2F values.
The AS2F model displays the same properties as the S2F model, except that it does not contain steps. The AS2F model is curved “upwards” long-term, compared to the time-based model.
The two decomposed S2F models are “bent” in the opposite direction of the S2F and AS2F models. This is due to the fact that the “aggressive” input variable is given a negative weight in the decomposed S2F models, whereas it has a positive weight in the S2F and AS2F models.
It is also interesting that the decomposed S2F (with steps) contains downward sloping periods. This is due to the “step” input variable, which also contains downward sloping periods. Once the overall slope of the model decreases sufficiently, the step variable starts to dominate, and the slope of the model price is negative.
In a semi-log scale, similar observations can be made:

The time-based model has perpetually diminishing growth. The S2F and AS2F models at first have diminishing growth but then transition to non-diminishing growth. According to these models, growth should currently be non-diminishing:
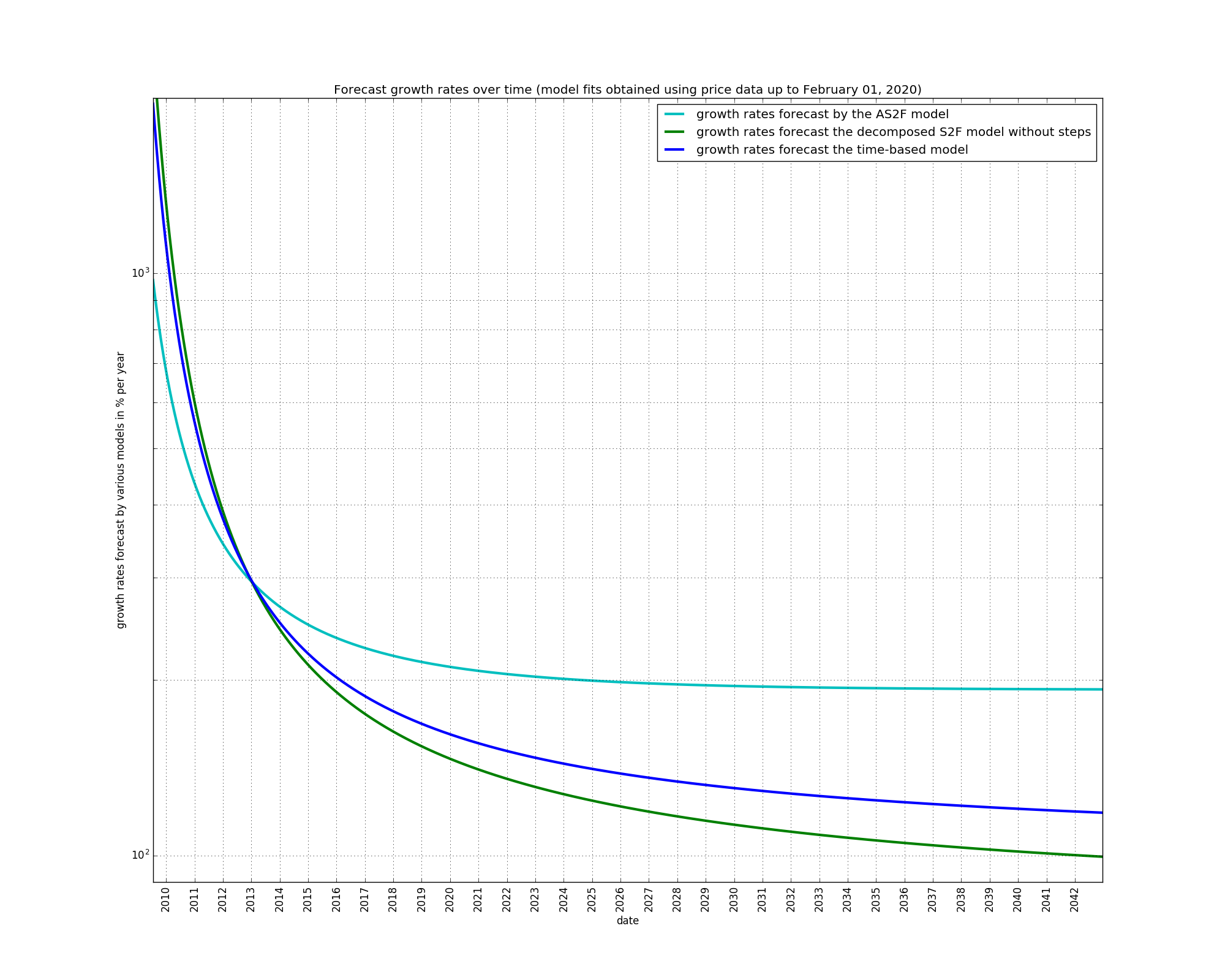
The decomposed S2F models have growth rates which are even more diminishing than those of the time-based model.
A final observation is that the early price data of 2009 is better fit by the models which have the growth which is the most diminishing, i.e. the decomposed S2F models better fit the early price data than the S2F and AS2F models.
Let’s see what the models forecast even further in the future:
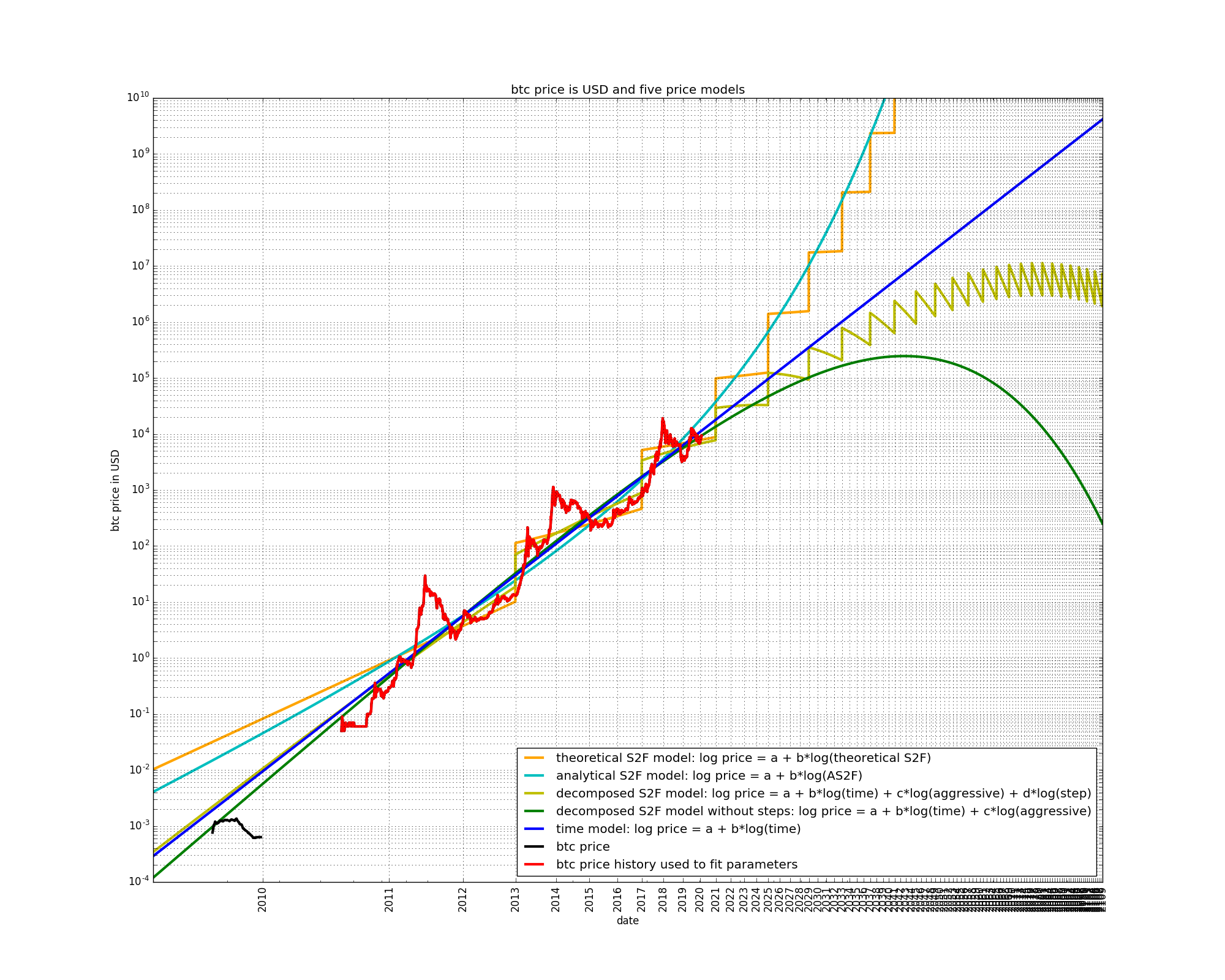
The S2F, AS2F, and time-based models do not present any particular surprises. However, the two decomposed S2F models forecast decreasing bitcoin prices. This is due to the negative weight assigned to the “aggressive” input variable.
We have seen that the “aggressive” variable at first grows slowly, but then ramps up quickly. This is due to its mathematical expression which contains an exponential:
![]()
Exponential growth eventually overtakes any other form of growth. If the exponential input variable is given a negative weight, the projected price will at some point decrease (and finally reach 0). A similar but opposite effect occurs if the exponential growth component is given a positive weight: positive exponential growth is non-diminishing. This means that any model that contains a positive exponential growth component without brakes will eventually be dominated by this component. This is the reason the S2F and AS2F models forecast non-diminishing growth.
The decomposed S2F models should not be interpreted as accurate price models. However, understanding what happens when each input variable is allowed to be weighted independently provides novel insight into the dynamics of the price evolution: If a component such as the “aggressive” variable is added to the time-based model, in terms of regression this component is best used in order to slow down the growth of bitcoin’s price, instead of accelerating it. In contrast, in the S2F price model, the “aggressive” variable is used to accelerate the price growth of bitcoin compared to the time-based model.
We have seen the models when the full history of bitcoin’s price data is used to fit their parameters:

Let us play time-traveller and observe how the five models behaved a while ago. We will just remove the last part of bitcoin’s price history to fit the model parameters:
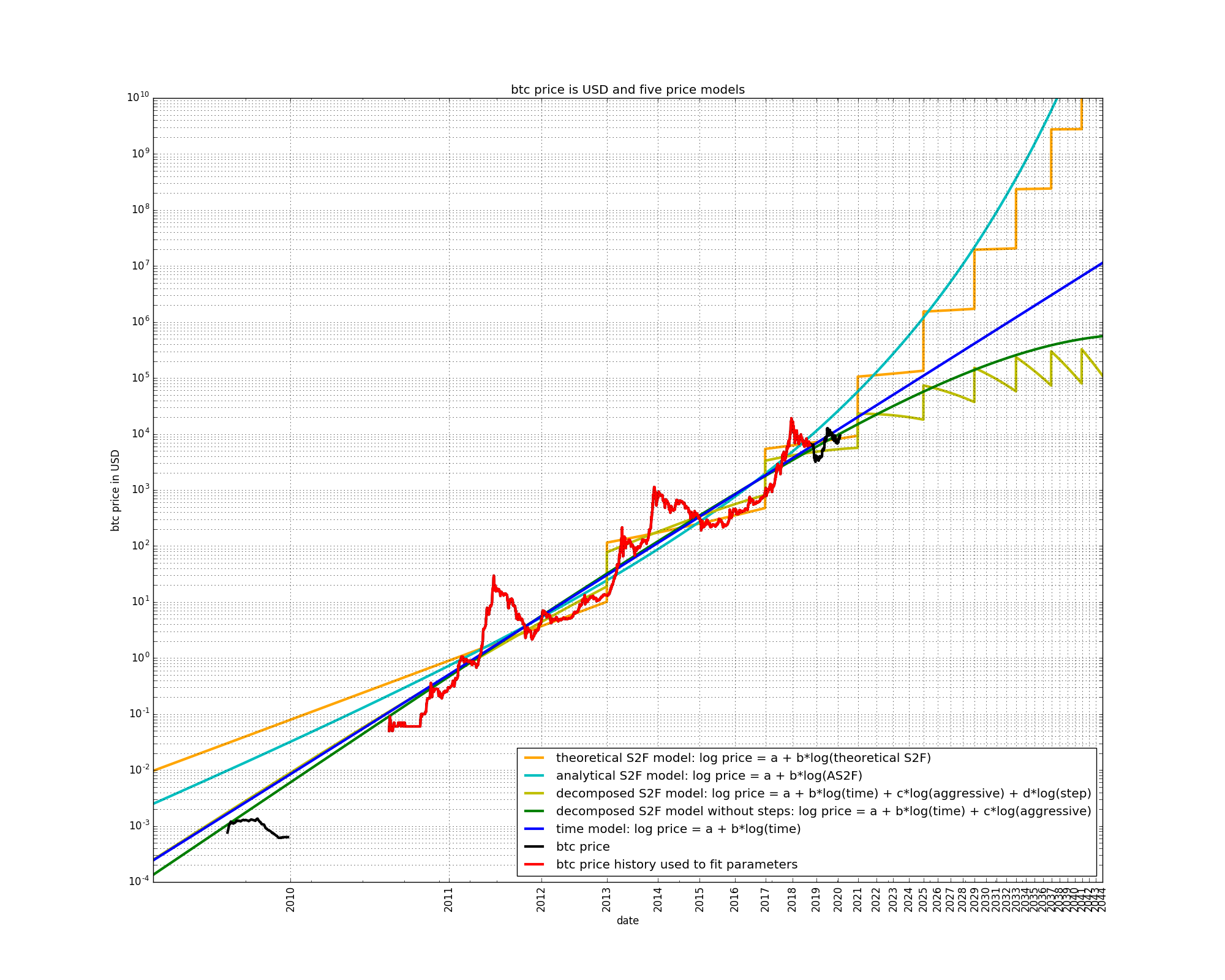
The predictions by the AS2F, S2F, and time-based models have not changed dramatically. So far, the two decomposed S2F models have not changed too much, either. However the decomposed S2F with steps now predicts lower prices than the decomposed S2F without steps.
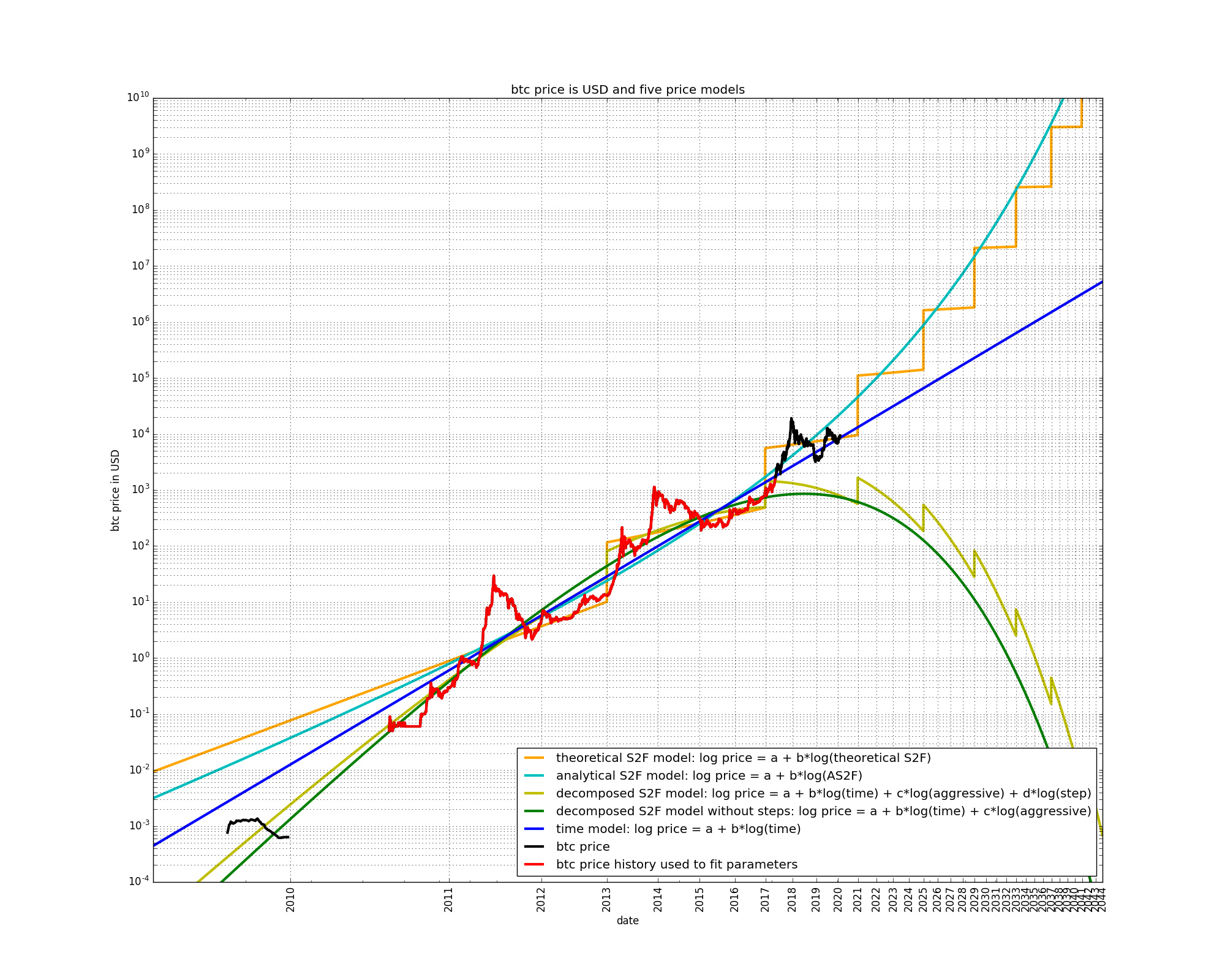
Removing some more data, the situation has again not changed much for the AS2F, S2F, and time-based models. The two decomposed S2F models now show a strong negative curvature.
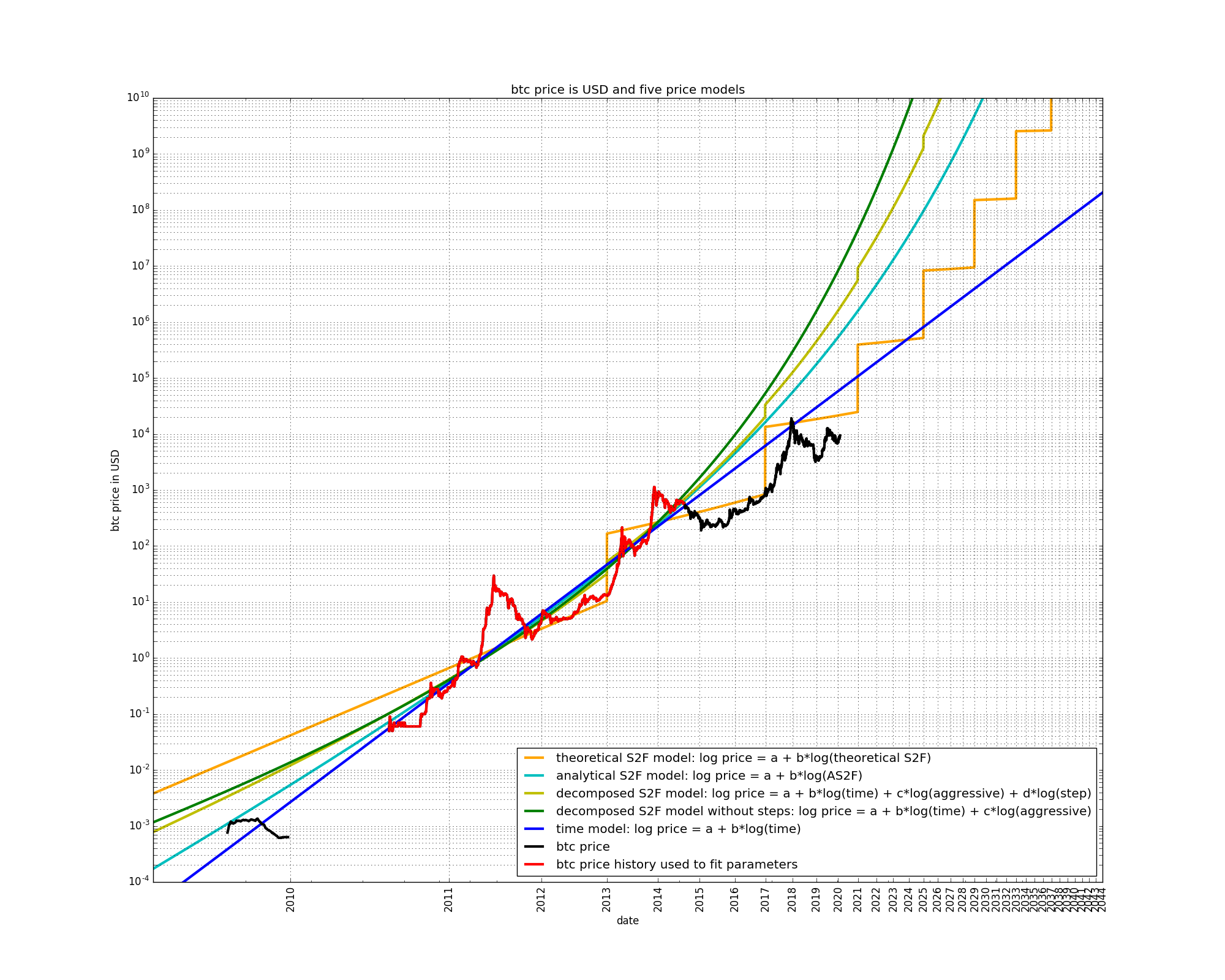
When yet more data is removed, the two decomposed S2F now predict higher prices than the AS2F, S2F, and time-based models!

When even more data is removed, the two decomposed S2F models do not agree with each other anymore. Also, the S2F model makes predictions that are too bullish.
This experiment illustrates the danger of using models containing the “aggressive” variable or any other exponential component. The two decomposed S2F models are especially unstable because the “aggressive” variable can be weighted independently of the other variables. Small variations in the weight of the “aggressive” variable can lead to large differences in forecast prices.
Let us use the decomposed S2F model without steps and examine the evolution of the weightings of the time and the “aggressive” variables:
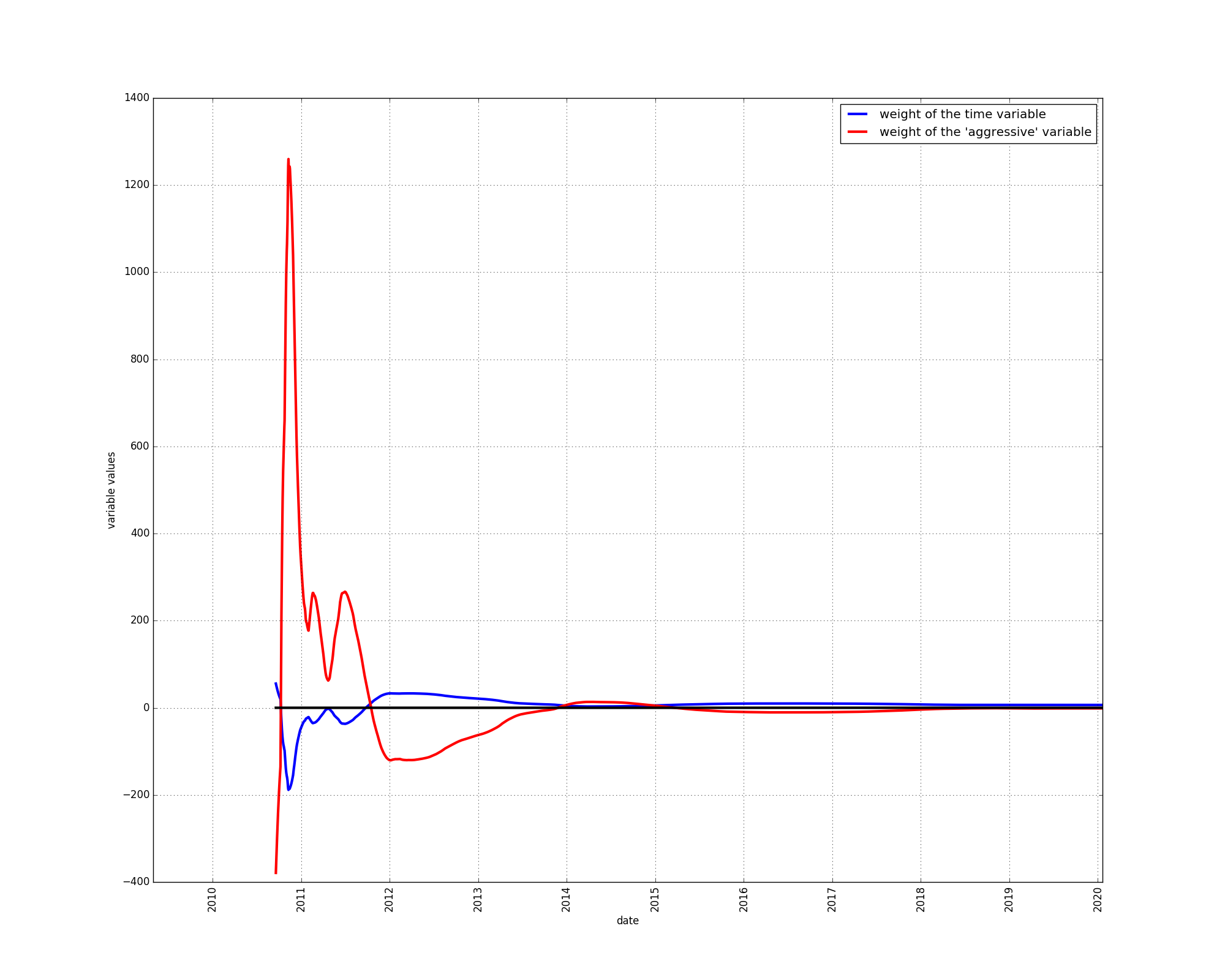
There was a period at the beginning of bitcoin’s price history, lasting from about the end of 2010 to the end of 2011 during which the price grew faster than adequately explained by the time-based model. The “aggressive” component therefore received a positive weighting.
During the year 2014, the same seemed to be the case. Price growth appeared to be faster than could be explained by the diminishing returns of the time-based model, hence the “aggressive” component received a positive weighting.
During the rest of bitcoin’s price history, the opposite has been the case: price growth appears to be slower than described by the diminishing returns of the time-based model.
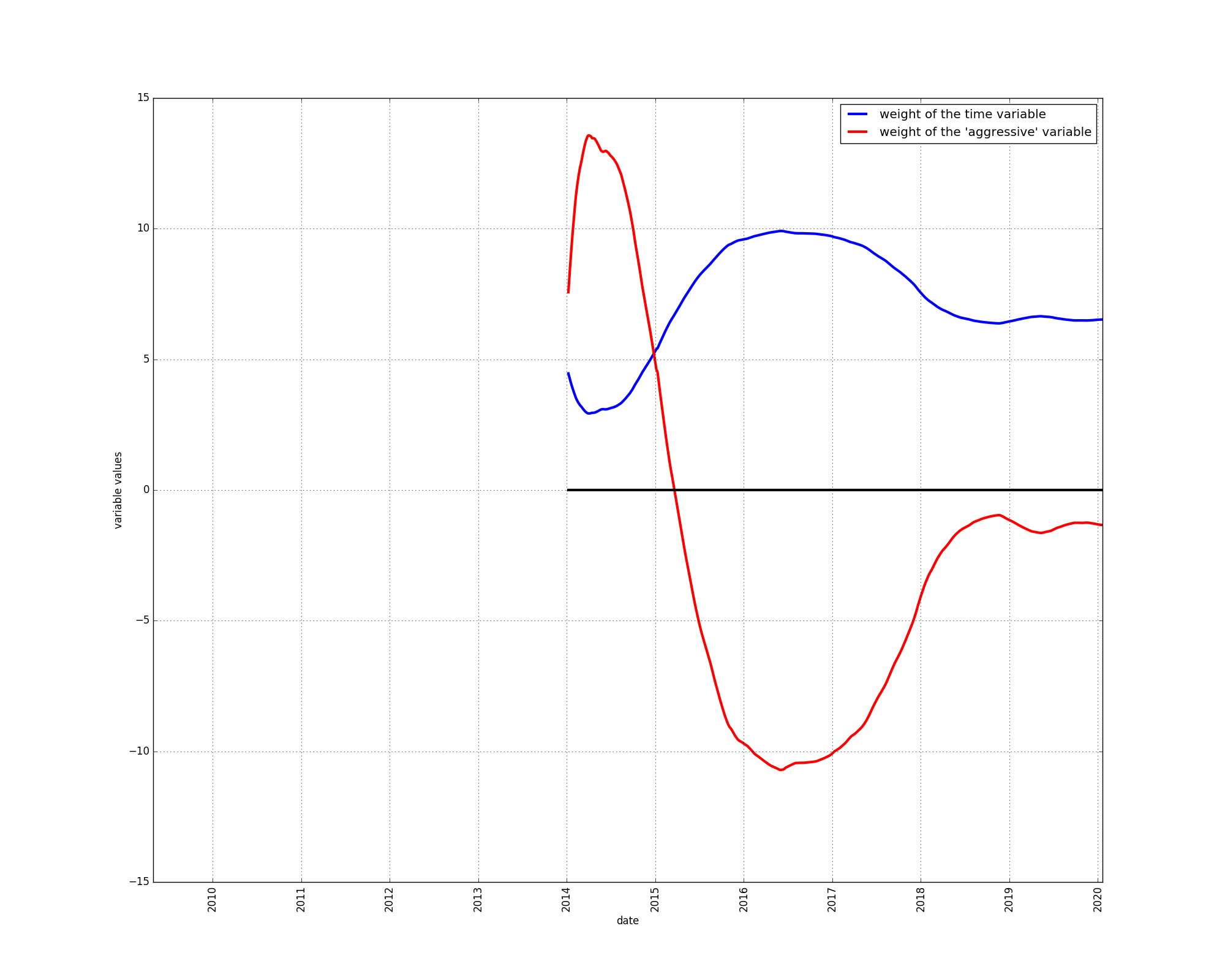
This situation has remained unchanged since the beginning of the year 2015, in spite of a major bull market in the year 2017.
This experiment reinforces our conclusion that the time-based model appears to be somewhat too bullish. The price data is better described using a component that slows down the growth of the time-based model.
Let’s repeat the above experiment for the decomposed S2F model with steps. We now have a third parameter value to plot: the weighting of the “step” component. The “step” input variable starts out at 1 at gradually decreases until the first halving (around the end of 2012) at which point it suddenly gets a value above 1.
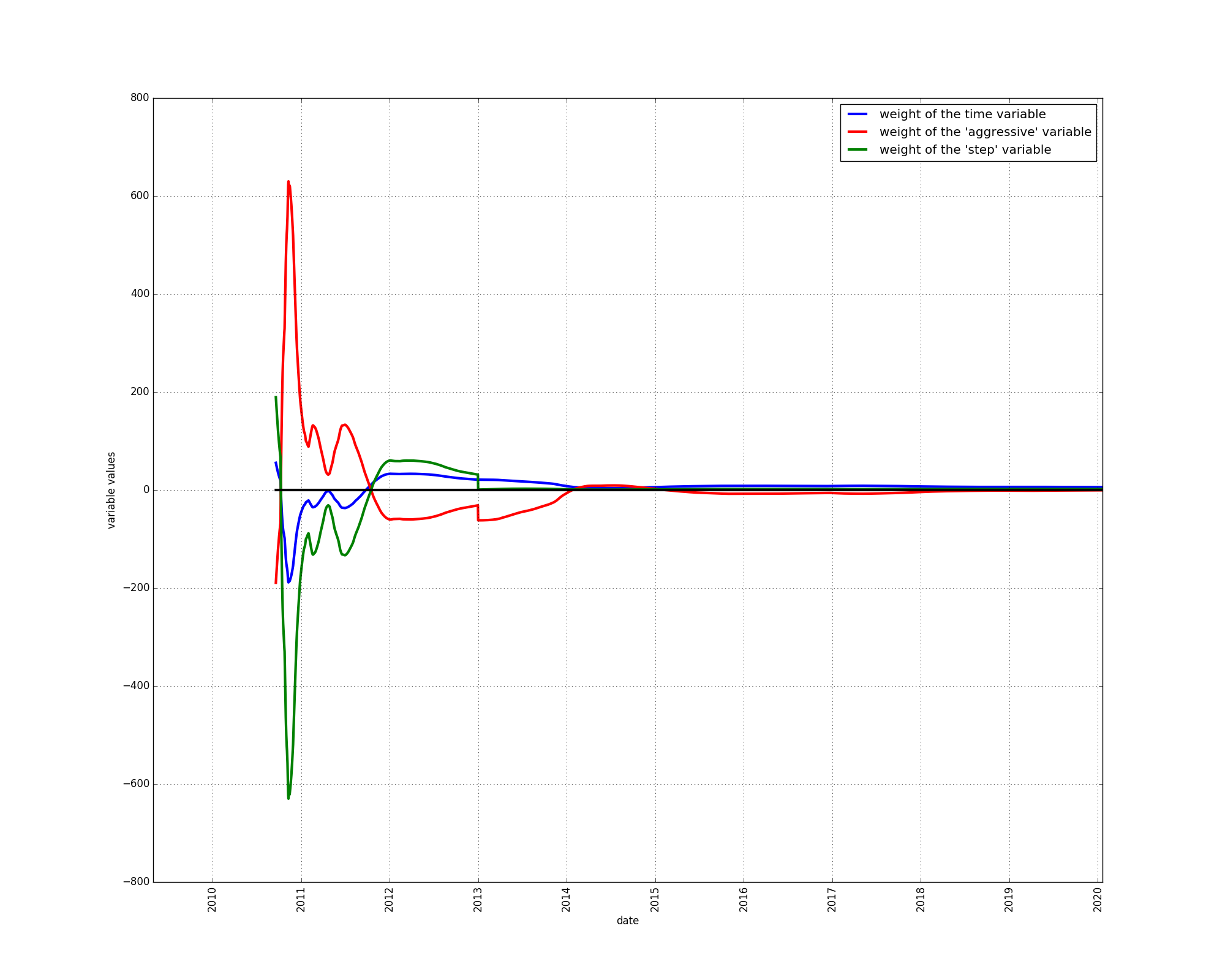
The step variable is given a positive weight starting in 2013, indicating that it is indeed useful in modelling the price. The step variable helps fit the bull markets.
For the weighting of the “aggressive” variable we observe virtually the same effect as in the decomposed S2F model without steps. The weighting is negative, with the same exceptions.

These two experiments show that the price not only has diminishing growth, but that the price would be better modeled using a model that has growth that diminishes faster than with the time-based model. This conclusion has remained unchanged since the beginning of 2015.
Our experiments indicate that bitcoin’s price has growth that diminishes faster than forecast by the time-based models proposed earlier by the authors of this article (here and here). The time-based models we formulated appear to be somewhat too bullish.
The S2F model forecasts non-diminishing growth and hence is much too bullish according to our findings. Inherently, the S2F model has a long-term trend which is incorrectly shaped: Price growth should slow down more and more, but the S2F model predicts price growth that stops diminishing.
The reason for the shape of the S2F model is due to the presence of an exponential component within the “aggressive” component, which is itself a component of the S2F variable itself. Exponentials are extremely dangerous when used without brakes. Intuitively, exponentials ultimately catch up with any other kind of growth. An exponential with a positive sign leads to non-diminishing growth forever, whereas an exponential with a negative sign leads to an ultimate bitcoin price of 0.
The decomposed S2F models have helped us assess whether bitcoin’s realized price could be better modelled using a model that grows either faster or slower than the time-based models, with the conclusion that growth should be slower.
The decomposed S2F models should not be used for actual price forecasts or trading purposes, due to their instability. The decomposed S2F models have more variables, and are therefore more prone to overfitting, a phenomenon we have observed by removing parts of bitcoin’s price history and projecting into the future. The fact that the partially exponential input variable can be weighted independently of the other variables makes the decomposed S2F models more unstable that the plain S2F model, in which the exponential component is coupled with other variables.
We thank Michael P. Frank for his excellent paper on deriving AS2F, Giovanni Santostani and BitcoinEconomics for their inputs in the manuscript, and we thank you for reading.